Méthodes d'hybridation Post-Quantique

Cet article complète un panorama de la transition post-quantique des produits certifiés.

Il est recommandé de commencer par sa lecture.

L’hybridation est la voie mise en avant par l’ANSSI, le BSI, l’AIVD et d’autres acteurs pour initier la transition aux algorithmes post-quantique. Combinant la résistance post-quantique des nouveaux algorithmes à la résistance classique éprouvée des actuels, elle permet une migration sans se reposer exclusivement sur des algorithmes et implémentations encore récents.

Un système hybride est construit de manière à rester sécurisé tant qu’au moins l’un des algorithmes sous-jacents n’est pas cassé. Afin de correctement avoir cette propriété, la méthode choisie pour l’hybridation doit être bien conçue.

Dans cet article, Oppida vous présente des méthodes d’hybridation reconnues et standardisées afin de pouvoir aborder la transition post-quantique de vos produits et certifications sereinement.

Confidentialité : hybridation de KEM

Dans l’article précédent, nous avons vu que les homologues post-quantique du chiffrement à clé publique (comme RSA) ou de l’échange de clé (comme Diffie-Hellman) sont pour la plupart des mécanismes d’encapsulation de clé (KEM). Les algorithmes classiques sont alors aussi considérés selon leurs variantes KEM, qui admettent déjà des standards couramment utilisés tels que RSA-KEM et ECIES.

Un KEM permet d’encapsuler une clé symétrique (comme une clé AES) via une clé publique, afin de la transmettre au détenteur de la clé privée, qui peut la décapsuler. Les deux utilisateurs peuvent alors chiffrer leurs communications à l’aide de la clé symétrique ainsi partagée. L’unique différence avec le chiffrement à clé publique est que la clé est fixée aléatoirement par le KEM, plutôt que par son utilisateur.

L’hybridation de KEM repose sur l’échange de deux clés en parallèle : l’un est réalisé avec un KEM pré-quantique, l’autre avec un KEM post-quantique. L’objectif est ensuite de combiner ces deux clés symétriques tout en garantissant que la clé combinée reste secrète même si l’un des deux KEM venait à être compromis. Dans l’article précédent nous avons vu que cette combinaison n’était pas complètement évidente, et en particulier que simplement concaténer ou XOR les clés ne suffisait pas à atteindre une sécurité satisfaisante. Une méthode sécurisée fera généralement intervenir une fonction de dérivation de clé (KDF), qui produit une clé de longueur souhaitée à partir d’un secret de taille arbitraire ; on peut par exemple utiliser HKDF, un KDF recommandé par l’ANSSI.

Les modes aujourd’hui les plus prometteurs sont CatKDF et CasKDF. Ceux-ci sont standardisés par l’ETSI, et repris par l’ANSSI dans son avis officiel.

CatKDF

Ce mode simple consiste essentiellement à concaténer les deux clés puis appliquer un KDF au résultat. Cependant d’autres informations supplémentaires sont également passées au KDF :

• les chiffrés produits par les encapsulations,
• les clés publiques en jeu,

et optionnellement :

• une clé pré-partagée (PSK),
• un séparateur de domaine,
• d’autres informations.

Il est important de passer les chiffrés au KDF¹. Les autres suppléments peuvent également améliorer la sécurité.

Le standard ne permet pour le choix du KDF que HKDF, avec une fonction de hachage parmi une liste de certaines fonctions SHA-2 et SHA-3.

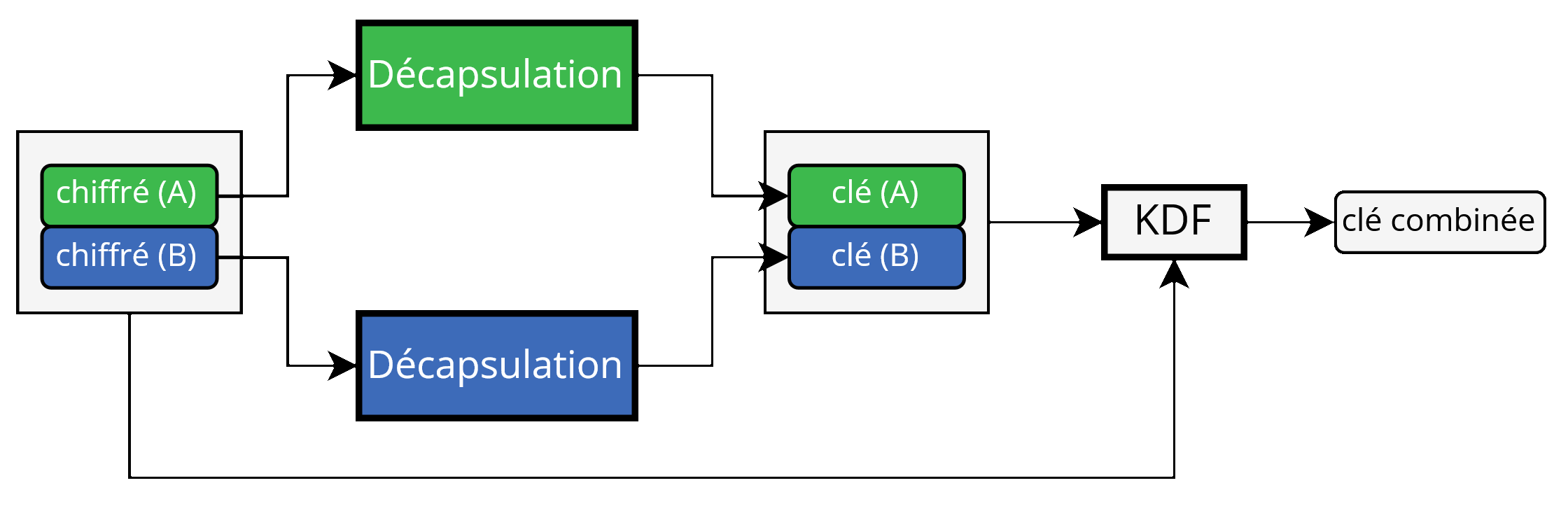Illustration de CatKDF utilisé par un destinataire. Les clés asymétriques et leur passage au KDF sont omis.

Cette approche est par exemple celle essentiellement adoptée par le futur design hybride de TLS, où la concaténation des clés partagées participe à une dérivation des clés de session par HKDF, ainsi notamment que les chiffrés et clés publiques via l’inclusion des messages qui les contiennent.

CasKDF

Le mode CasKDF (Cascade KDF) produit une clé symétrique en utilisant un procédé sous forme de cascade qui accepte une clé intermédiaire supplémentaire par itération. Il y a autant d’itérations que de KEM combinés.

Comme pour CatKDF, des informations supplémentaires aux clés décapsulées sont passées au KDF :

• les chiffrés produits par les encapsulations,
• les clés publiques en jeu,

et optionnellement :

• une clé pré-partagée (PSK),
• un séparateur de domaine,
• d’autres informations.

À nouveau, il est important de passer les chiffrés au KDF¹, et les autres suppléments peuvent également améliorer la sécurité. Une autre différence avec CatKDF est l’usage additionnel d’un PRF, qui dans le standard est simplement instancié avec HMAC.

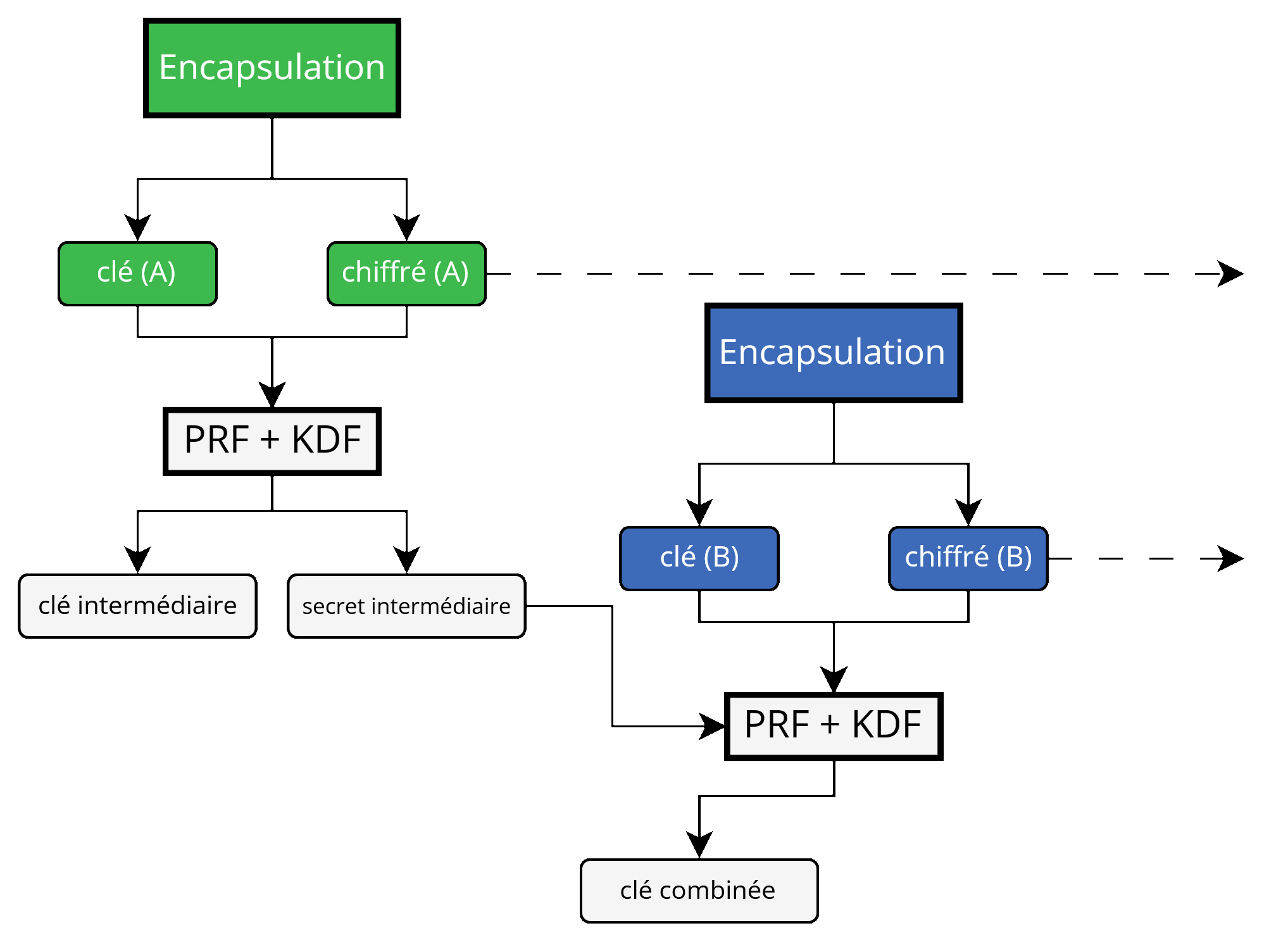Illustration simplifiée de CasKDF utilisé par un émetteur. Les clés publiques et leur passage au PRF sont omis.

Outre de potentiels avantages logistiques tels que la réduction de l’empreinte en mémoire et la séparation des messages, la génération itérative de la clé symétrique peut éventuellement permettre le chiffrement des messages intermédiaires par les clés intermédiaires ; ce qui est documenté par le standard.

Les messages étant toujours indépendants et simplement séparés par rapport à CatKDF, ils peuvent tout autant être envoyés en même temps sans attendre de réponse, et en particulier ce mode est tout autant approprié à un contexte hors-ligne que CatKDF. Par rapport à CatKDF, CasKDF pour deux KEM coûte 2 appels de PRF et 1 appel de KDF supplémentaires, mais le coût de ces appels est assez faible en comparaison aux opérations des KEM.

Utilisation de clés éphémères

Lors de sa mention de ML-KEM et FrodoKEM dans son avis, l’ANSSI émet les recommandations suivantes :

1. Il est important d’éviter de modifier les paramètres de l’instance normalisée.

2. Les paramètres sont définis pour plusieurs niveaux de sécurité. Nous recommandons d’utiliser le niveau de sécurité NIST le plus élevé possible, de préférence le niveau 5 (équivalent à l’AES-256) ou le niveau 3 (équivalent à l’AES-192).

3. Nous recommandons d’utiliser autant que possible des clés éphémères. L’utilisation systématique de clés privées éphémères permet de prévenir de nombreuses attaques telles que les attaques utilisant des oracles d’échecs de déchiffrement.

4. Nous recommandons également d’utiliser la version sécurisée contre les attaques actives (IND-CCA) qui sera normalisée par le NIST. Dans certains cas, comme dans les protocoles authentifiés disposant de preuves de sécurité, la version sécurisée contre les attaquants passifs (IND-CPA) en mode statique ou éphémère peut être considérée comme sûre. Mais il faut alors veiller à ce qu’aucun oracle d’échec de déchiffrement ne soit disponible en toutes circonstances, même en cas d’attaque par canaux auxiliaires.

Les deux premiers points sont assez simples : ces schémas font l’objet de paramétrages minutieux qui ont été fixés et analysés par les chercheurs, et il vaut donc mieux se tenir à ceux-ci ; accessoirement, les changer compliquerait l’interopérabilité. Les niveaux encouragés sont quant à eux des prises de position conservatrices.

Le dernier point est également relativement simple : ces schémas sont d’abord construits comme des chiffrements à clé publique, qui sont ensuite transformés en un KEM ; la transformation en question permet alors d’affirmer un niveau de sécurité plus élevé. L’ANSSI (et bien d’autres) recommande de s’en tenir à ce KEM final plutôt qu’une de ses briques cryptographiques, mais reconnaît l’existence de cas particuliers où la sécurité supplémentaire en question serait superflue en théorie, ce qu’il convient alors de vérifier.

Le troisième point recommande d’utiliser des clés éphémères, le plus possible. Ceci admet plusieurs raisons :

Confidentialité persistante (PFS)

Une fois qu’une clé éphémère est oubliée pour toujours par le système, la (ou les) clé de session qu’elle a protégé ne peut plus être retrouvée, même si les secrets du système sont volés par une compromission. Cette propriété est classiquement garantie dans TLS 1.3, et peut être réalisée avec des KEM post-quantique par les mêmes méthodes.

Réduire la surface d’attaque d’une clé

Des vulnérabilités d’une implémentation ou déploiement telles que des canaux auxiliaires pourraient permettre d’attaquer la clé utilisée. De telles attaques bénéficient voire nécessitent souvent plusieurs interactions avec la clé. Si la clé ne sert qu’un très petit nombre de fois, ces attaques en souffrent.

Plus loin, elles peuvent complètement disparaître si une clé éphémère ne sert toujours qu’une fois : il ne coexiste alors pas une session normale que l’attaquant souhaite décrypter, et une session que l’attaquant perturberait pour glaner des informations sur la clé.

Les niveaux de sécurité supérieurs² des KEM étudiés et de leurs méthodes d’hybridation nécessitent des arguments (relativement) moins standards pour être prouvés. La sécurité IND-CCA des KEM ML-KEM ou FrodoKEM est prouvée en se plaçant dans le ROM ou QROM. De même, la sécurité IND-CCA de CatKDF ou CasKDF nécessite de se placer dans le ROM ou d’admettre d’autres hypothèses, et elle n’est pas encore démontrée dans le QROM. Ceci peut également motiver une réduction de la surface d’attaque concernée en réduisant l’utilisation d’une même clé.

Par ailleurs, si une telle attaque a un coût non négligeable et ne sert à casser qu’une seule clé, rendre celle-ci éphémère implique qu’elle couvre moins d’informations, et vaut moins la peine de surmonter ce coût. Vu autrement, le coût d’une attaque visant à recouvrer un ensemble d’informations est fortement augmenté si ces informations sont protégées par des clés distinctes moins exposées qu’il faut casser individuellement.

L’alternative des clés pré-partagées (PSK)

Les modes CatKDF et CasKDF présentés précédemment admettent l’option d’ajouter aux dérivations une clé pré-partagée (PSK). Dans leur définition, ceci se veut une défense en profondeur et optionnelle ; CasKDF nécessite d’ailleurs explicitement au moins deux tours, ce qui signifie faire intervenir au moins deux KEM.

Pour autant, il est envisageable de réaliser une hybridation ne faisant intervenir que :

1. une PSK,
2. un KEM classique, non post-quantique.

Cette technique garantit bien une résistance post-quantique, car repose sur le paradigme de la cryptographie symétrique, et a l’intérêt d’être très facilement réalisée dès aujourd’hui : elle ne fait intervenir que des mécanismes classiques éprouvés, et peut par exemple déjà être réalisée avec une configuration appropriée de TLS.

Si cette approche est suivie, l’ANSSI émet les avertissements suivants :

1. La confidentialité et l’intégrité de la clé pré-partagée sont des conditions préalables essentielles.

2. Chaque clé pré-partagée ne doit être partagée que par deux parties et non pas par un groupe de trois parties ou plus.

3. La confidentialité parfaite dans le temps (abrégé par PFS en anglais) n’est pas garantie contre les adversaires quantiques (car la sécurité reposera sur un secret long-terme).

La notion de PFS a été présentée précédemment. Un adversaire quantique, qui a un CRQC à sa disposition, saura déjouer le KEM classique et pourra déchiffrer toutes les communications passées à la moindre compromission de la PSK.

Authenticité : hybridation de signatures

Dans l’article précédent, nous avons vu que les algorithmes actuels de signature électronique pouvaient être cumulés en hybridation à des algorithmes post-quantique afin de résister aux CRQC.

L’hybridation de signatures est essentiellement plus simple que celle des KEM, les concaténer permet déjà d’atteindre un niveau de sécurité généralement satisfaisant.

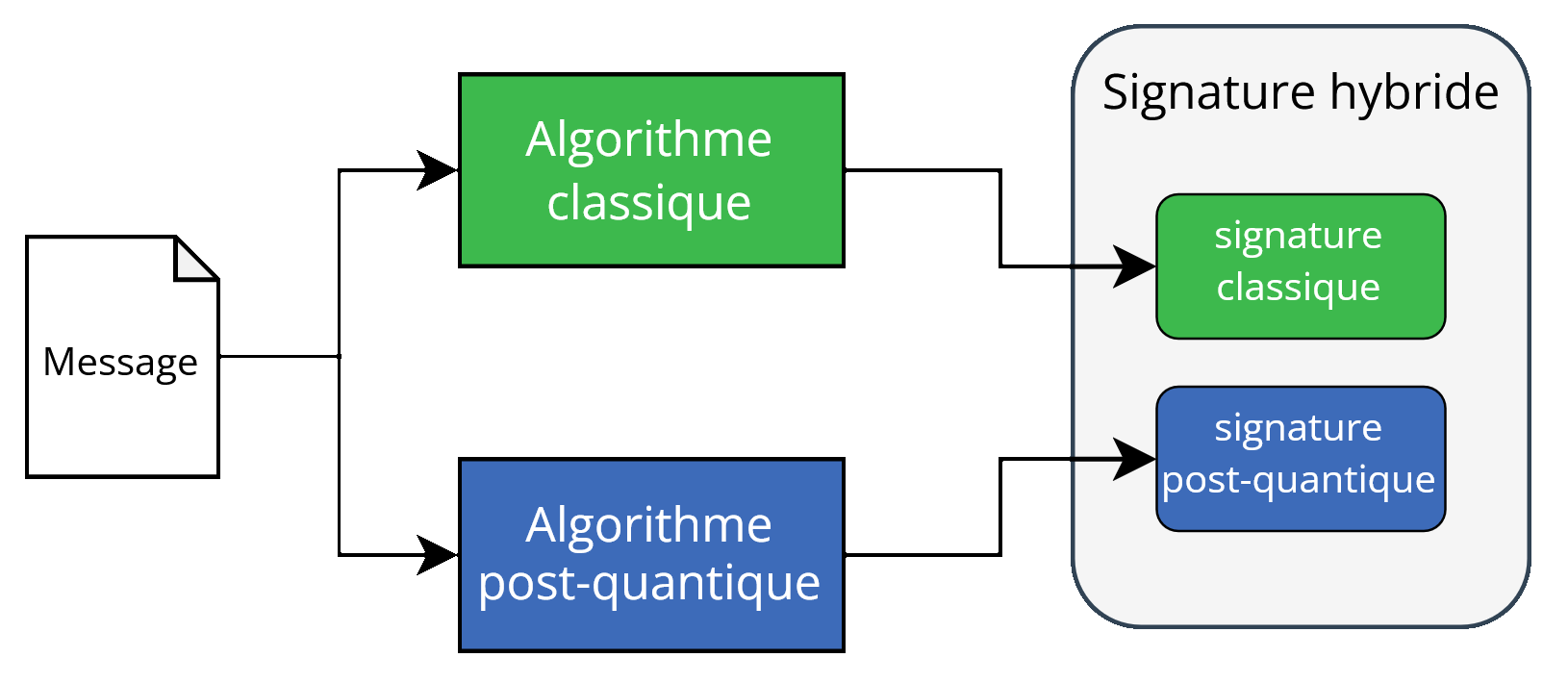Génération d’une signature hybride. Deux signatures sont indépendamment réalisées et concaténées.

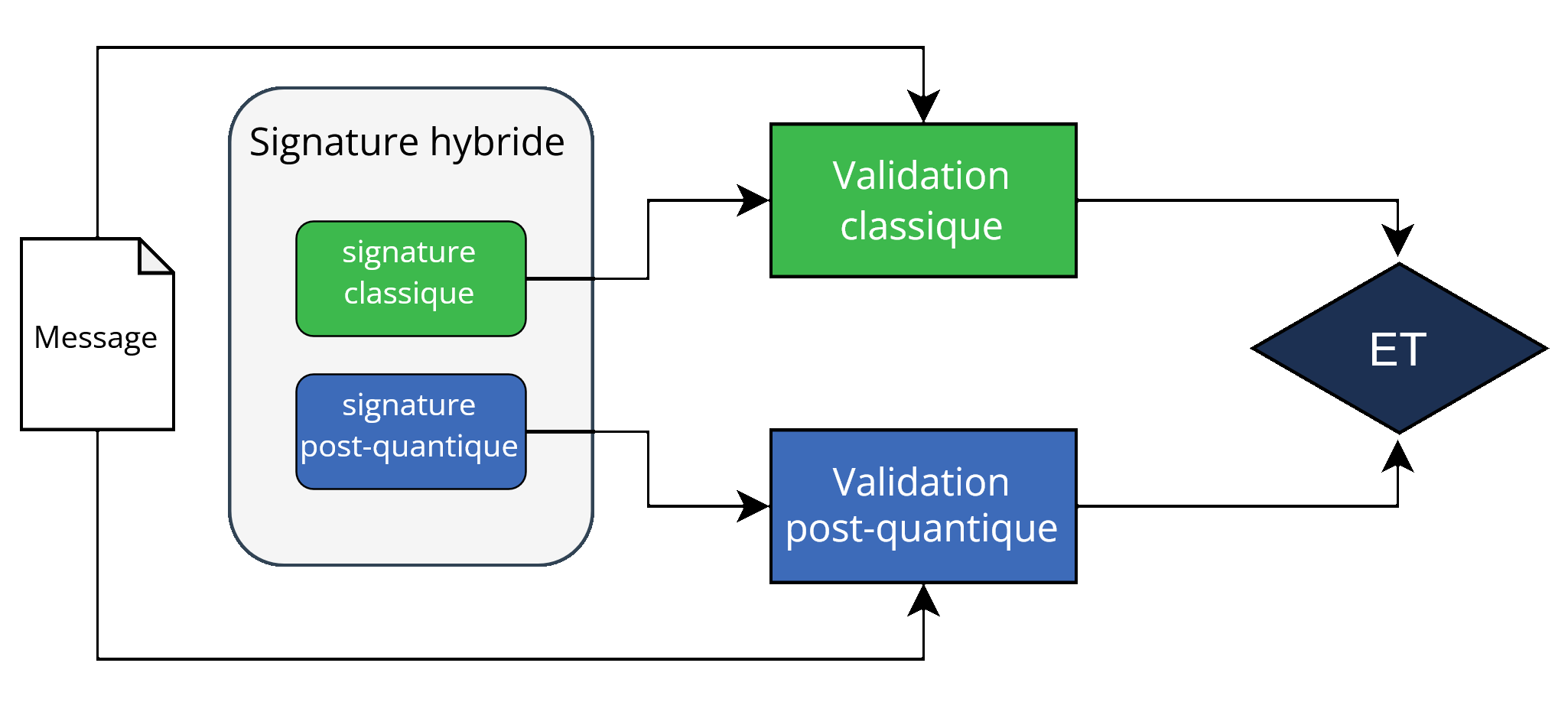Vérification d’une signature hybride. Les deux signatures sont indépendamment vérifiées.

Cette approche est notamment formalisée par l’ETSI sous le nom “concatenation only”.

Précisément, cette approche atteint le niveau de sécurité EUF-CMA, qui signifie qu’un attaquant ne peut pas produire de signature valide d’un message jamais signé ; tant qu’au moins l’un des schémas sous-jacents atteint ce niveau. Pour autant, il existe des propriétés de sécurité supplémentaires que l’on peut espérer d’un algorithme de signature hybride.

Non-séparabilité

La méthode décrite précédemment admet une particularité : en générant une signature hybride utilisant deux algorithmes de signature, on expose des signatures valides pour les algorithmes individuels. Il est alors possible pour un attaquant qui l’intercepte de transformer une signature hybride en une signature seulement classique ou seulement post-quantique, ce qui n’était pas l’intention de leur émetteur. Si le système de destination traite les signatures hybrides et classiques différemment, ceci peut alors constituer une vulnérabilité, exploitable sans ordinateur quantique.

De tels systèmes risquent justement d’exister au cours de la transition à la cryptographie post-quantique. En effet, ils pourraient accepter :

• des signatures hybrides,
• des signatures post-quantique pures,
• des signatures classiques pures, pour rétrocompatibilité.

Ces risques peuvent être éliminés par une bonne gestion des clés, précisant par exemple qu’une clé publique ne peut être utilisée que dans un contexte d’hybridation précis, et pas pour une signature existant seule. Il est également possible d’utiliser des techniques d’hybridation plus complexes ne permettant pas de telles attaques.

Une approche simple est de reprendre le même schéma d’hybridation que précédemment, mais de le lier aux schémas utilisés ; ce que l’on peut faire en intégrant les identifiants des algorithmes au message signé. À la vérification du message par certains algorithmes, le vérificateur rajoute les identifiants nécessaires, et la signature n’est valide sur le tout que pour la bonne combinaison. Cette approche est notamment formalisée par l’ETSI sous le nom “concatenation with identifiers”³. 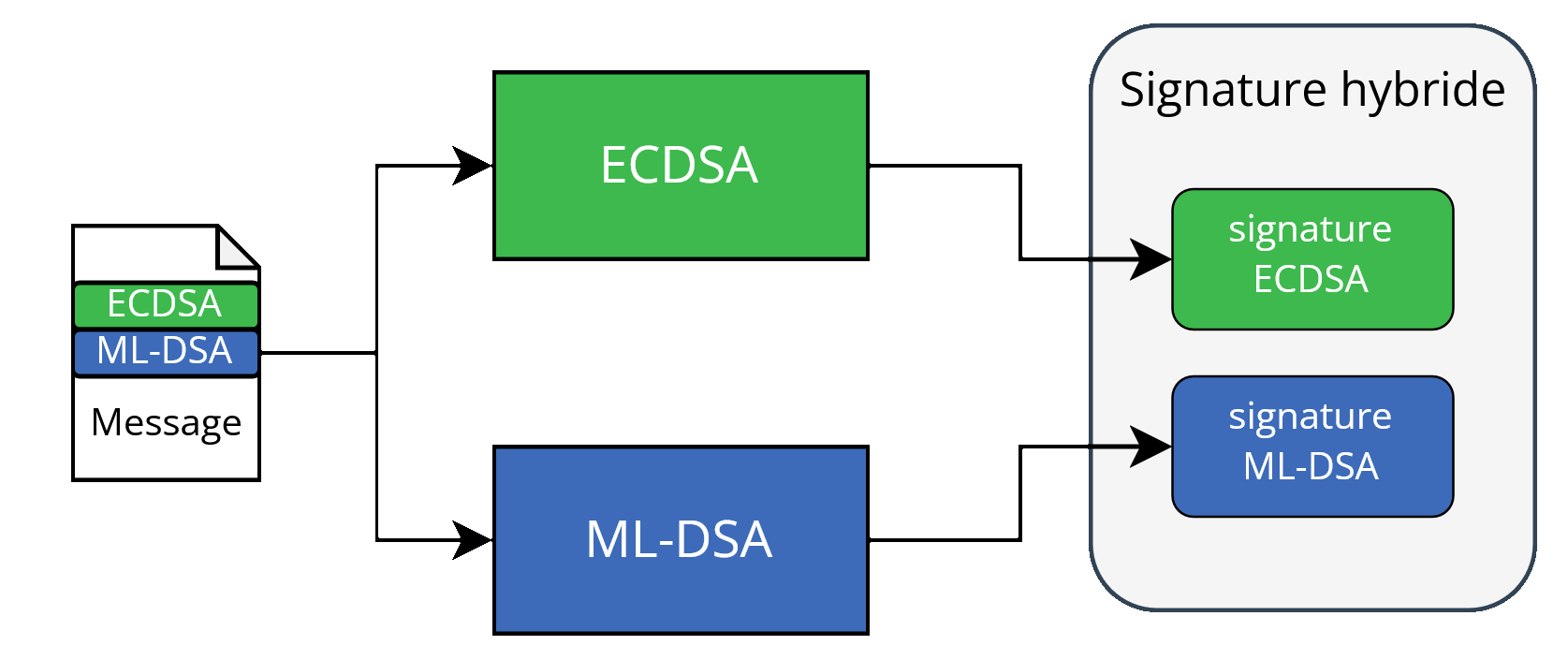Exemple d’une hybridation avec identifiants utilisant ECDSA et ML-DSA : la signature porte sur les identifiants et le message.

Sécurité forte

Par rapport au niveau EUF-CMA atteint par l’approche par concaténation, il existe aussi le niveau SUF-CMA, qui signifie qu’un attaquant ne peut pas concevoir une signature jamais émise par le système ; y compris pour un message déjà signé par le passé. La capacité de modifier des signatures légitimes peut présenter un problème selon les hypothèses qu’utilise un système, et peut par exemple faciliter des attaques par rejeu dans certains contextes.

La cryptomonnaie Bitcoin a été historiquement sujette à une malléabilité de ses transactions qui pourrait permettre la répétition malveillante de paiements ; une source de malléabilité étant l’algorithme de signature ECDSA qui n’atteint par défaut pas le niveau SUF-CMA.

Les approches d’hybridation par concaténation n’atteignent pas ce niveau de sécurité, quand bien même les algorithmes sous-jacents l’atteindraient. Il suffit par exemple d’intervertir les composantes de deux signatures hybrides d’un même message pour violer la propriété.

De nombreux autres critères de sécurité existent pour les mécanismes de signature électronique, et il convient de déterminer ceux nécessités par un système, potentiellement par des hypothèses qu’il ferait implicitement pour sa sécurité. Certains peuvent être atteints par des transformations génériques plus ou moins complexes d’un mécanisme établi.

L’alternative des clés pré-partagées (PSK)

De même que pour la confidentialité, des clés pré-partagées (PSK) offrent un moyen post-quantique d’assurer l’authenticité de données et communications. Mieux encore, à l’inverse de la confidentialité, cette approche ne cause pas une absence de PFS, et ne nécessite pas de procéder à une hybridation comme elle est éprouvée.

En effet, cette approche est aujourd’hui et depuis longtemps déjà utilisée et facilement déployable dans un système maîtrisé de bout en bout, supportée par exemple par des protocoles tels que TLS et IKE.

Les premiers avertissements de l’ANSSI continuent cependant de s’appliquer :

1. La confidentialité et l’intégrité de la clé pré-partagée sont des conditions préalables essentielles.

2. Chaque clé pré-partagée ne doit être partagée que par deux parties et non pas par un groupe de trois parties ou plus.

Face à la difficulté de migrer rapidement les infrastructures à clés publiques à des mécanismes de signature post-quantique, cette approche peut être une bonne solution temporaire à court terme, dans les systèmes qui s’y prêtent.

Pour autant, elle ne remplace pas certains usages des signatures qui leur sont propres, tels que la signature de document. Une PSK ne permet pas de prouver une authenticité à un autre acteur, sans lui céder cette même capacité de preuve.

Références

1. Avis scientifique et technique de l’ANSSI sur la migration vers la cryptographie post-quantique, ANSSI, avril 2022
2. Avis de l’ANSSI sur la migration vers la cryptographie post-quantique (suivi 2023), ANSSI, décembre 2023
3. Cryptographic Mechanisms: Recommendations and Key Lengths, BSI, février 2024
4. The PQC Migration Handbook, TNO,CWI,AIVD, décembre 2023
5. ISO/IEC 18033-2:2006: Technologies de l’information — Techniques de sécurité — Algorithmes de chiffrement ; Partie 2: Chiffres asymétriques, ISO, mai 2006
6. Guide de sélection d’algorithmes cryptographiques, ANSSI, mars 2021
7. Quantum-safe Hybrid Key Exchanges, ETSI, décembre 2020
8. Security of Hybrid Key Encapsulation, Cryptology ePrint Archive, janvier 2021
9. Hybrid key exchange in TLS 1.3 draft-ietf-tls-hybrid-design-12, NWG, janvier 2025
10. Deployment Considerations for Hybrid Schemes, ETSI, octobre 2024
11. On the Malleability of Bitcoin Transactions, Financial Cryptography and Data Security, janvier 2015

---

1. Certaines des preuves de sécurité associées aux modes CatKDF et CasKDF reposent sur l’intervention de ces informations, notamment leurs preuves IND-CCA dans le ROM. Intuitivement, dans le ROM, inclure les chiffrés dans le KDF implique qu’un attaquant ne peut pas manipuler ceux-ci tout en ayant que la même clé symétrique est produite. ↩︎ ↩︎²

2. On entend ici IND-CCA, la définition courante de sécurité contre un attaquant pouvant manipuler des chiffrés. ↩︎

3. Cette approche ne fournit qu’une non-séparabilité faible, à savoir qu’un attaquant peut toujours extraire une signature valide du message, mais dans laquelle réside des artéfacts de l’hybridation. D’autres approches permettent de réaliser une non-séparabilité forte où l’attaquant n’apprend aucune signature valide pour un algorithme sous-jacent seul, mais ces approches nécessitent de modifier les algorithmes utilisés et peuvent restreindre les algorithmes supportés. ↩︎